Уровень моря

Если, находясь на берегу моря, наблюдать за поверхностью воды, то выяснится, что граница между сушей и водой непрерывно передвигается. Вода то наступает на берег, то отступает, т. е. какая-то зона суши заливается или осушается. Эта зона называется переходной зоной между морем и сушей. Её ширина зависит от рельефа берега и от размаха колебаний уровня и меняется от ничтожно малых колебаний уровня при скалистых берегах до десятков и даже сотен километров в районах отмелых берегов и значительных колебаний уровня моря.

Колебания уровня моря оказывают влияние на многие стороны деятельности человека, на формирование рельефа береговой зоны моря, развитие и существование жизни в прибрежной зоне. Для многих практических целей крайне важно (например, гидротехническое строительство) знать положение трёх линий:

• линия, начиная с которой дно никогда не обнажается;
• средняя линия, т. е. линия между сушей и водой при среднем уровне;
• линия, выше которой никогда воды не бывает.

Положение этих линий соответствует наинизшему, среднему и наивысшему уровням. Определение этих характерных уровней является одной из основных задач исследования уровня.

Большое влияние оказывает уровень и на судовождение в прибрежной зоне моря. В некоторых районах плавание возможно только в определённые промежутки времени. При заходе в подавляющее число портов мира судоводитель обязательно должен знать положение уровня моря.

Таким образом, для исследования уровня, использования его в практических целях необходимо определить его как числовую величину.

Инженерное определение уровня следующее: уровень моря — это высота невзволнованной поверхности (т. е. поверхности, свободной от ветровых волн и зыби) над условной плоскостью, принятой за нулевую. На морях, где величина прилива составляет 50 см и более, высота уровня отсчитывается от нуля глубин.

Уровенная поверхность

Вид и форма поверхности морей и океанов формируется под воздействием различных сил. Основная сила, действующая на водную оболочку Земли, — это сила тяжести. Под её воздействием частицы воды стремятся занять положение покоя или равновесия. Поверхность, соответствующая этому положению, т. е. поверхность нормальная к направлению силы тяжести, называется уровенной поверхностью или поверхностью геоида.

Другие действующие силы стараются вывести частицы воды из состояния покоя. Все их можно разделить на три группы:

• периодические приливообразующие силы Луны и Солнца;
• комплекс сил, обусловленных гидрометеорологическими факторами, т. е. явлениями, происходящими в атмосфере и гидросфере;
• силы, обусловленные процессами, протекающими в земной коре.

Все эти силы нарушают равновесие частиц воды и возбуждают все виды движения в Мировом океане. Каждому из этих видов движения соответствует своё определённое положение поверхности воды, которое не совпадает с уровенной поверхностью. Вследствие этого наблюдать в океане уровенную поверхность или точную поверхность геоида невозможно. Поэтому условно принято считать, что уровенная поверхность совпадает с поверхностью среднего многолетнего уровня моря в каком-либо пункте (там, где имеются такие наблюдения). В России, например, уровенная поверхность проходит через «0» Кронштадтского футштока, положение которого близко к среднему многолетнему уровню Балтийского моря в Кронштадте.

Виды колебаний уровня, наблюдаемые в Мировом океане

Перечисленные выше три группы сил, воздействующие на воды океана, вызывают следующие виды колебаний уровня:

1. Приливообразующие силы Луны и Солнца возбуждают периодические колебания поверхности воды, наиболее правильные во времени и достаточно хорошо изученные. Им посвящено огромное количество работ, они наблюдаются во всех морях и океанах. Подробные сведения о них будут изложены в следующих разделах.

2. Гидрометеорологические факторы вызывают следующие виды колебаний уровня:

• сгонно-нагонные колебания, возникающие в результате действия ветра на водную поверхность;
• статические изменения уровня вследствие изменения атмосферного давления;
• изменение уровня, вызванное нарушением баланса в звеньях влагооборота (испарения, осадков, стока). В результате в море может увеличиваться или уменьшаться количество воды, а, следовательно, изменяется уровень.

Все перечисленные виды колебаний являются непериодическими и имеют разную величину. Наиболее существенными являются сгонно-нагонные колебания. Их величина зависит от рельефа дна и конфигурации береговой линии. Наибольшей величины сгонно-нагонные колебания достигают у отмелых берегов и в длинных сужающихся к берегу заливах. Нередко эти колебания имеют характер стихийного бедствия. Сгонно-нагонные колебания совпадают, как правило, с изменением уровня под воздействием атмосферного давления. Такое комплексное явление, т. е. нагон вод в сочетании с волновыми колебаниями, вызванными резким изменением давления при прохождении барических систем, обуславливает наводнения в Санкт-Петербурге.

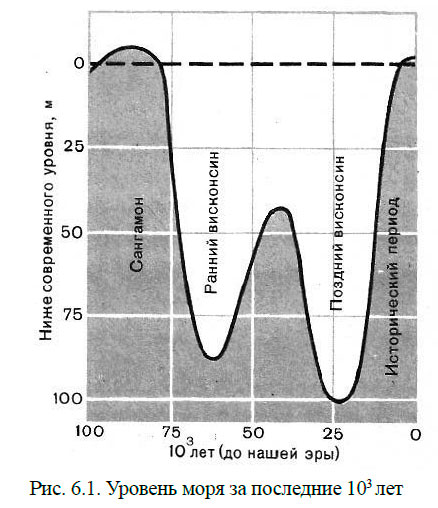
3. Силы, обусловленные процессами, происходящими в земной коре, носят глобальный характер. В результате их действия береговая линия на протяжении геологической истории Земли меняла своё положение по отношению к современному, которое мы наблюдаем сейчас. Примерно 17 тыс. лет назад уровень Мирового океана был ниже современного, море отступило от берегов (регрессия), и береговая линия находилась в районе нынешней бровки шельфа. Следы древних береговых линий можно обнаружить на шельфах морей и океанов. Затем началась трансгрессия (наступление моря на сушу), и примерно 4 тыс. лет тому назад уровень Мирового океана был примерно на 4 м выше современного. Это наглядно видно в экваториальных широтах, там, где берега сложены остатками колониальных кораллов.

Данные археологии также свидетельствуют о том, что не всегда материки имели такие очертания, как сейчас. На дне морей находят следы пребывания человека. Эти глобальные, долгопериодные изменения уровня Мирового океана могут быть вызваны вертикальными смещениями земной коры, изменением общего количества воды в Мировом океане или совместным действием этих процессов (рис. 6.1).

Приливные колебания уровня моря

ОБЩИЕ СВЕДЕНИЯ О ПРИЛИВАХ

В результате взаимодействия в пределах солнечной системы Земли, Луны и Солнца на нашей планете наблюдаются явления, названные приливными. Они выражаются в периодических изменениях уровня в любой точке Мирового океана и возникновении течений. Колебания уровня называются приливами, а течения — приливными течениями.

Явление прилива заключается в следующем: уровень воды постепенно поднимается, что называется приливом, достигает наивысшего положения, которое называется полной водой (ПВ) и начинает понижаться. Процесс понижения уровня называется отливом. Понижаясь, уровень достигает наиболее низкого положения, которое называется малой водой (МВ), а затем снова начинает повышаться. Наблюдения над уровнем морей и океанов в различных пунктах нашей планеты показывают, что в течение суток в одних районах может наблюдаться две полных и две малых воды, а в других одна полная и одна малая. В первом случае приливы называются полусуточными, во втором — суточными.

Промежуток времени между двумя последующими полными или малыми водами называется периодом прилива. Полусуточные приливы имеют период, равный половине лунных суток, т. е. 12 ч. 25 мин. Период суточных приливов равен лунным суткам (24 ч. 50 мин.). Перечисленные выше характеристики можно наглядно видеть на рис. 6.2, на котором показано изменение уровня в течение суток (от 0 час. до 23 час.). Дополнительно к перечисленным, прилив характеризуется следующими параметрами:

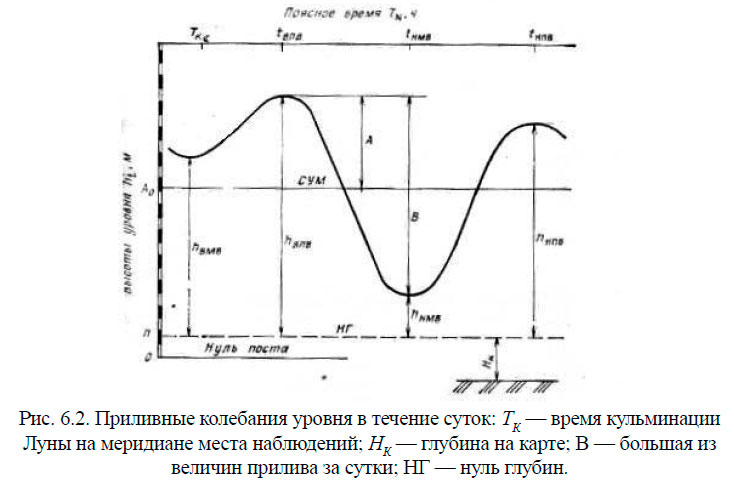
• величина прилива — разность уровней соседних полной и малой вод;
• высота прилива — положение приливного уровня по отношению к нулю глубины;
• время полной воды — момент наступления полной воды;
• время малой воды — момент наступления малой воды.

И в заключение отметим, что термин «прилив» употребляется в двух значениях: как название всего явления и как название отдельного его процесса, а именно, повышения уровня.

НЕРАВЕНСТВА В ЯВЛЕНИИ ПРИЛИВОВ

Наблюдая за величиной прилива и временами наступления полных и малых вод в каком-либо пункте, можно заметить, что они меняются день ото дня и даже в течение суток. Отклонение величин прилива и времени наступления полных и малых вод от средних значений называются неравенствами прилива. Выделяют следующие виды неравенств в явлении приливов:

1. Суточные неравенства. Они проявляются в различии по высоте двух смежных полных и малых вод в течение суток и в неравенстве роста и падения уровня. В связи с этим вводятся дополнительные термины (рис. 6.2):

• высокая полная вода (ВПВ) — бóльшая из двух полных вод за сутки при полусуточных приливах;
• низкая полная вода (НПВ) — меньшая из двух полных вод за сутки;
• высокая малая вода (ВМВ) — бóльшая из двух малых вод за сутки;
• низкая малая вода (НМВ) — меньшая из двух малых вод за сутки.

Таким образом, различают суточное неравенство высот полных вод и суточное неравенство высот малых вод там, где наблюдаются полусуточные приливы.

Суточные неравенства приливов зависят от склонения Луны. Наибольшие по величине наблюдаются при максимальном склонении, наименьшие — при склонении равном нулю.

2. Полумесячные неравенства. Прилив, который мы наблюдаем, представляет собой сумму лунного и солнечного приливов. Направление приливообразующих сил Луны и Солнца непрерывно изменяется вследствие вращения Луны вокруг Земли и Земли вокруг Солнца. В течение месяца направление от Земли к Солнцу изменяется мало, так как Земля делает полный оборот вокруг Солнца за 365 дней. Направление же на Луну за месяц меняется на 360°, т. е. Луна делает полный оборот вокруг Земли. В результате этого дважды в месяц Луна, Земля и Солнце находятся на одной прямой. На Земле мы отмечаем эти моменты как новолуние и полнолуние и называем их сизигиями. Дважды в месяц направление на Луну будет перпендикулярно направлению на Солнце — первая и последняя четверть. На Земле в эти моменты мы наблюдаем половину лунного диска — это квадратуры. Луна и Солнце действуют самостоятельно и производят свои эллипсоиды прилива.

В течение месяца эти эллипсоиды складываются различным образом, но в сизигии большие оси лунного и солнечного эллипсоидов совпадают и тогда к поднятию уровня от лунного прилива прибавляется поднятие от солнечного. Одновременно от лунной малой воды отнимается солнечная малая вода. В результате получается наибольшая величина прилива в месяц. Такие приливы называются сизигийными.

В квадратуры, когда направление на Луну перпендикулярно направлению на Солнце, большие оси эллипсоидов приливов будут перпендикулярны друг другу. Солнечному приливу будет соответствовать лунный отлив, а лунный прилив совпадёт с солнечным отливом. В результате высота суммарного прилива уменьшается, а суммарного отлива увеличивается. В результате величина прилива бывает наименьшая за месяц. Это квадратурные приливы.

Кроме полумесячных неравенств в величине приливов наблюдаются полумесячные неравенства во времени наступления полной воды сизигийного прилива. Полная вода соединённого, т. е. сизигийного прилива, наступает не в момент астрономической сизигии, а спустя некоторое время после неё (чаще всего 1–3 суток). Этот промежуток называется возрастом полусуточного прилива.

3. Параллактическое неравенство (месячное). Это неравенство зависит от изменения расстояния между Землёй и светилами, т. е. Луной и Солнцем. Луна движется вокруг Земли не по круговой орбите, а по эллиптической. Один раз в месяц она бывает в наибольшем удалении от Земли (апогей) и один раз — в наименьшем (перигей). Следовательно, сила притяжения Луны меняется от наибольшей в перигее до наименьшей в апогее.

4. Длиннопериодные неравенства:

• солнечное тропическое полугодового периода, обусловлено кажущимся годовым движением Солнца;
• годовое солнечное параллактическое, зависящее от параллакса Солнца;
• неравенство с периодом 18,61 года, обусловленное склонением Луны.

Классификация приливных режимов

Приливы в Мировом океане отличаются очень большим разнообразием. Однако, несмотря на это, можно выделить несколько характерных типов приливов, которые наблюдаются в том или ином районе Мирового океана, т. е. классифицировать приливы. В нашей стране в основе классификации лежат следующие признаки приливов:

• количество полных и малых вод в течение суток;
• величина и характер суточных и полумесячных неравенств;
• симметрия в нарастании и спаде уровня.

Формальным критерием для отнесения приливов к той или иной группе является соотношение

где Н_К1 и Н_О1 — амплитуды главных суточных волн прилива; Н_М2 — амплитуда главной полусуточной волны.

В зависимости от величины этого критерия можно выделить следующие типы приливов:

1. Полусуточные приливы при 0 < K < 0,5. Они характеризуются тем, что в каждые сутки бывает две полных и две малых воды. Период прилива в среднем равен 12 ч. 25 мин. Высоты полных и малых вод отличаются мало, т. е. суточные неравенства малы. Время роста и падения уровня практически одинаковы. Изменение величины прилива связано с фазами Луны (полумесячные неравенства). В дни новолуний и полнолуний наблюдаются самые высокие полные воды и самые низкие малые воды в течение месяца. Следовательно, величины приливов будут наибольшие. Это сизигийные приливы.

В последующие за сизигией дни высоты полных вод уменьшаются, а высоты малых вод увеличиваются и с переходом Луны во II-ю или IV-ю четверть наблюдаются самые малые высоты полных вод и самые высокие малые воды. В результате величины приливов становятся наименьшими. Это квадратурные приливы. Хорошо выраженные полусуточные приливы наблюдаются в Атлантическом океане.

2. Смешанные приливы — это наиболее сложные по характеру колебаний типы приливов. В течение месяца все признаки явления изменяются. Смешанные приливы делятся на две группы — неправильные полусуточные и неправильные суточные:

а) неправильные полусуточные приливы ближе к полусуточным. В течение месяца они, в общем, имеют две полных и две малых воды. Однако при максимальном склонении Луны вторые полные и малые воды незначительны насколько, что прилив только условно можно считать полусуточным. С увеличением склонения Луны нарушается симметрия между высотами полных и малых вод, т. е. время роста и падения уровня неодинаково, увеличиваются суточные неравенства. При уменьшении склонения Луны суточные неравенства уменьшаются, и при прохождении Луны через экватор приливы имеют характер почти правильных полусуточных. Неправильные полусуточные приливы распространены в Индийском и Тихом океанах. Величина критерия таких приливов находится в пределах 0,5 < K < 2,0;

б) неправильные суточные приливы характеризуются критерием 2,0 < K < 4,0. У этих приливов преобладают особенности суточных приливов. Основные признаки обусловлены склонением Луны. При прохождении Луны через экватор наблюдаются почти правильные полусуточные приливы с двумя полными и двумя малыми водами в лунные сутки. Величина приливов в это время наименьшая. С увеличением склонения Луны очень быстро увеличиваются суточные неравенства. Наступает момент, когда ВМВ и НПВ практически исчезают, и приливы на некоторое время становятся суточными с одной полной и одной малой водой. При наибольшем склонении Луны величина приливов становится максимальной. Приливы этого типа чаще всего встречаются в бассейне Тихого океана: Татарский пролив, Курильские острова, побережье Камчатки и другие места.

3. Суточные приливы с критерием К > 4,0. У этих приливов в течение суток наблюдается одна полная вода и одна малая. Таким образом, период явления равен одним лунным суткам. Подъём и падение уровня происходят по вполне симметричной косинусоидальной кривой. Эта симметричность нарушается во время прохождения Луны через экватор. В этот момент плавный рост или падение уровня может нарушаться и какое-то время уровень не меняется (стояние уровня). При малых склонениях Луны наблюдаются также и наименьшие величины приливов. Когда Луна находится в своём наибольшем склонении, величины приливов достигают наибольших значений.

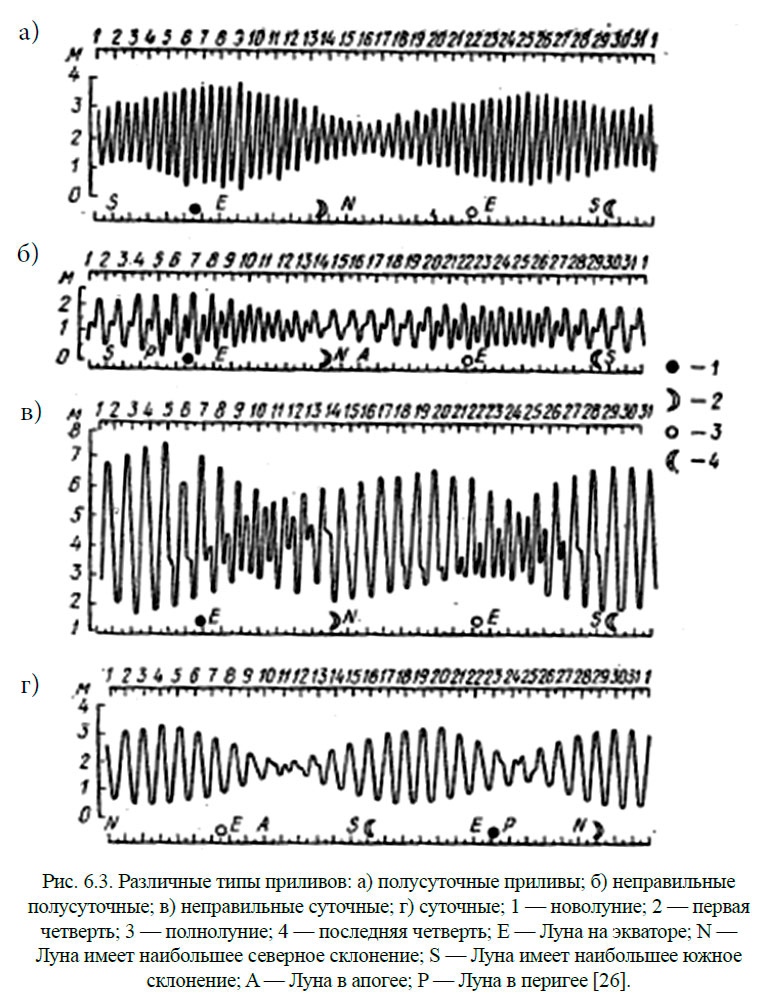
Все перечисленные типы приливов показаны на рис. 6.3.

Аномальные приливы. Рассмотренные выше типы приливов относятся к основным. В некоторых пунктах Мирового океана наблюдаются приливы, которые отличаются от основных отдельными признаками, что позволяет считать их аномальными.

Полусуточные солнечные имеют период, равный 12 часам. Поэтому полные и малые воды наблюдаются в одно и то же время.

Полусуточные параллактические приливы отличаются от полусуточных основных характером полумесячных неравенств. Высоты и величины приливов меняются не в зависимости от фаз Луны (сизигия, квадратура), а в зависимости от расстояния между Землёй и Луной. При наименьшем расстоянии наблюдаются наибольшие величины приливов и наоборот. Такие приливы наблюдаются в заливе Креста в Беринговом море.

Иногда приливы становятся двойными полусуточными, т. е. в течение суток бывает четыре полных и четыре малых воды. Примером могут быть приливы в Портленде и Саутгемптоне.

Аномальные приливы на побережье Мирового океана встречаются редко.

Значительное влияние на приливы оказывает мелководье. Наиболее заметно мелководье сказывается на полусуточных приливах: нарушается симметрия подъёма и спада уровня; кривая подъёма становится круче кривой спада.

Больше всего явление прилива искажается в устьевых участках рек. На некоторых реках, куда входит приливная волна, наблюдается особое явление, которое носит название бор (английское) или маскарэ (французское). При движении волны прилива вверх по реке её передний склон становится практически вертикальным, обрушивается, а затем распространяется вверх по реке в виде пенящегося вала высотой от одного до нескольких метров. Иногда бор сопровождается сильным шумом. После прохождения этой волны уровень продолжает повышаться так, как при обычном приливе. Как правило, бор наблюдается не ежедневно, а только в сизигию. Явление бора наблюдается на некоторых реках Англии, Франции, в устье Ганга высота бора достигает 2 м, на Амазонке — 3,5–4,5 м. В нашей стране бор бывает на р. Мезень и называется манихой.

После прекращения бора приливная волна распространяется вверх по реке дальше. Верхняя граница распространения приливной волны может достигать нескольких сотен километров, а на р. Амазонка прилив распространяется на 1400 км.

Основные сведения из теории приливов

Существование периодических колебаний уровня моря было известно не менее четырёх тысяч лет назад. Первые описания приливов известны нам из трудов мыслителей античности. Там же мы находим указания о влиянии движения Луны на приливы. Однако до открытия закона всемирного тяготения И. Ньютоном (1642–1727) причины явления приливов оставались неизвестными. Ньютон дал объяснение явлению приливов, определил величину приливообразующих сил, показал причины главных неравенств в явлении приливов. Это были основы так называемой «статической теории» приливов. С тех пор и до настоящего времени продолжается работа над созданием законченной теории приливов. Свой вклад в эту работу внесли выдающиеся учёные всех времён и народов: Д. Бернулли, П. С. Лаплас, В. Томсон, Д. Х. Дарвин, А. Т. Дудсон, Д. Картрайт и др. Разработкой ряда вопросов теории приливов занимались отечественные учёные: М. В. Никитин, В. В. Шулейкин, А. И. Берёзкин, Н. Н. Зубов, Н. П. Владимирский, А. И. Дуванин, И. В. Максимов, А. В. Некрасов и др.

ПРИЛИВНОЙ ПОТЕНЦИАЛ

Приливообразующая сила определяется как результирующая двух сил: силы притяжения элементарной массы в точке Р (произвольная точка на поверхности Земли) и силы притяжения Луной и Солнцем такой же массы в центре Земли. Для сокращения и простоты рассуждения обычно рассматривают возмущающее действие Луны, так как для Солнца все выводы будут аналогичны. Далее вместо анализа самой силы сначала находят выражение её потенциала. Зная потенциал, легко найти силу. Применение потенциала удобно по следующим причинам. Потенциал равен потенциальной функции, взятой с обратным знаком. Потенциальная функция — такая функция координат точки, частные производные которой по осям x, y, z равны составляющим силы по направлениям этих осей. Поскольку направления осей x, y, z ничем не обусловлены (т. е. мы задаём их сами), то при замене их какими-либо другими координатами можно определить проекции силы в любом направлении. Далее находится приливной потенциал. Его нахождение иллюстрируется рис. 6.4.

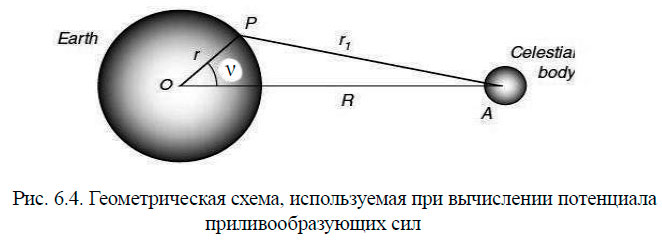
На рисунке через ν обозначено зенитное расстояние Луны, приведённое к центру Земли. Окончательно выражение приливообразующего потенциала Луны запишем по работе, заменив обозначение потенциала «Ω», применяемого в работе, на чаще встречающееся в литературе по приливам «V»:

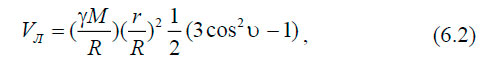
где γ — гравитационная постоянная; М — масса Луны; r — расстояние между центром Земли и точкой P; R — расстояние между Луной и центром Земли.

Переменная ν связана с локальной системой координат, что не даёт возможности выполнить разложение потенциала на различные приливные составляющие. Поэтому выбираются более удобные экваториальные координаты и cosν выражается через часовой угол Т, склонение δ светила (Луны) и φ, λ — астрономические координаты места наблюдений. Окончательно получим:

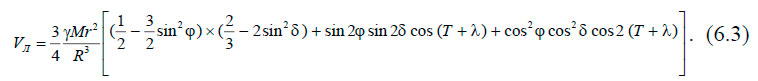
Впервые такое разложение потенциала было выполнено Лапласом. Как видно, потенциал V_л представляет собой сумму трёх членов, что даёт возможность разделить приливы на три вида:

1) полусуточные приливы, которые описываются членами 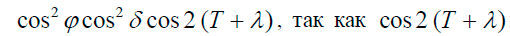имеет период изменения практически равный ½ суток;

2) суточные приливы, содержащие sin 2φ sin2δ cos (T + λ);

3) долгопериодные приливы, содержащие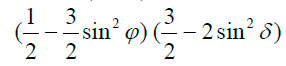

так как склонение и параллакс возмущающего тела (Луны, Солнца) изменяются сравнительно медленно.

Дальнейшее развитие теории приливов шло по пути анализа приливного потенциала. Его члены не содержат достаточно удобного разложения потенциала приливных сил. Склонение, расстояние до возмущающего тела, часовой угол представляют сами собой сложные функции времени. Эти функции нужно было представить тригонометрическими рядами и выразить потенциал суммой гармоник, характеризующихся своей амплитудой и аргументом, связанным линейной зависимостью с гринвичским средним солнечным временем и восточной долготой λ. Каждый член гармонического ряда имеет конкретную физическую причину, определяемую фундаментальными периодами орбитального движения Земли и Луны:

• периодом изменения лунного склонения (27,321582 суток);
• периодом изменения солнечного склонения (365,242199 суток);
• периодом обращения лунного перигея (8,847 лет);
• периодом обращения лунного узла (18,613 лет);
• периодом обращения перигелия (20,940 лет).

Первое чисто гармоническое разложение потенциала было выполнено Дудсоном и содержит 396 волн; последнее на момент написания этой работы — Д. Картрайтом и др. и состоит из 509 волн. Из всего набора гармоник в табл. 6.1 представлены гармоники, имеющие наибольшие амплитуды. При этом необходимо иметь в виду, что при выводе потенциала предполагалось, что суша отсутствует.

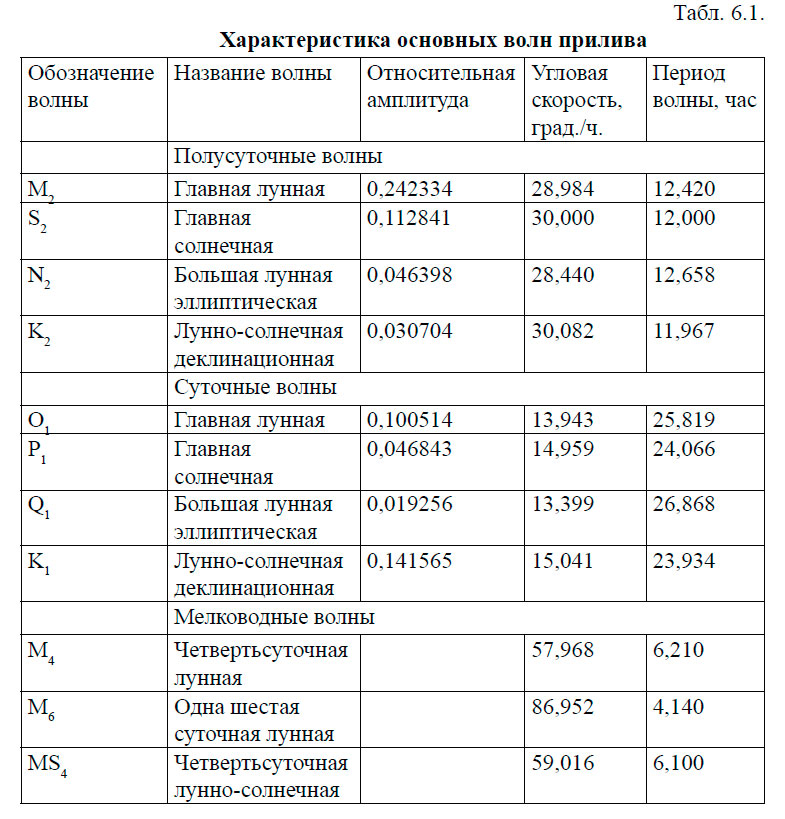
Предвычисление приливов

Если бы условия на нашей планете соответствовали принятым допущениям при выводе потенциала приливообразующих сил, то задача их предвычисления была бы существенно проще. Приливы по своей природе являются волнами большой длины. Их скорость зависит от глубины моря. Перемещаться со скоростью Луны относительно земной поверхности они не могут. Кроме этого, свободному распространению волны препятствуют континенты. Проблема предвычисления приливов требует решения двух различных задач. Первая задача — это разработка метода предвычисления приливов в пунктах, где ведутся наблюдения за уровнем. Вторая — предвычисление приливов на обширных пространствах Мирового океана с большими глубинами и отсутствием пунктов наблюдений.

ПРЕДВЫЧИСЛЕНИЯ ПРИЛИВОВ НА ПОБЕРЕЖЬЕ МАТЕРИКОВ И ОСТРОВОВ

Для предвычисления приливов в пунктах побережий, где ведётся систематическая регистрация уровней мареографами (приборы для измерения уровня воды), используется гармонический метод. Гармоники, используемые для расчёта высоты прилива, выбираются заранее из числа разложения потенциала. Каждая волна представляется в виде:

где fH — амплитуда волны; q — угловая скорость волны в один час среднего времени в градусах; t — среднее солнечное время; (V₀ + u−g°) — начальная фаза волны.

Амплитуда и начальная фаза волны состоят из двух частей: астрономической (теоретической) и местной, зависящей от местных физико-географических условий:

• f — редукционный множитель, медленно изменяющийся из года в год (астрономический параметр);
• Н — средняя амплитуда приливной гармоники, её величина зависит от местных условий и для конкретного места остаётся постоянной (если не происходит заметных изменений этих условий);
• (V₀ + u) — часовой угол приливообразующего светила на момент времени t (астрономический параметр);
• g° — угол положения волны, зависящий от местных условий. Для конкретного места постоянный.

Величины Н и g были названы гармоническими постоянными.

Для предвычисления прилива необходимо найти гармонические постоянные для всех волн, которые выбираются для расчёта. Астрономические аргументы на «0» часов первого для расчёта находятся по формулам в зависимости от:

• средней долготы Луны;
• средней долготы Солнца;
• долготы перигея лунной орбиты;
• долготы восходящего узла лунной орбиты;
• долготы перигелия.

Для определения гармонических постоянных необходимы наблюдения. Точность определения гармонических постоянных, их количество и, следовательно, точность расчётной высоты прилива будет зависеть от длительности этих наблюдений. Из 19-летней серии наблюдений можно получить до 400 волн, из годовой серии — 170–200 волн, из месячной — до 35 волн. В настоящее время для определения гармонических постоянных используется метод наименьших квадратов. Приведём пример. Будем считать, что для представления прилива достаточно 8 основных волн (четыре полусуточных и четыре суточных). В этом случае предвычисление прилива ведётся по формуле:

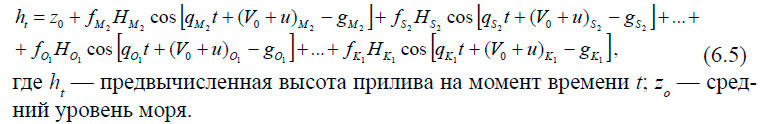
Уравнение содержит всего 9 членов. При использовании большего числа волн количество членов в уравнении будет увеличиваться.

Точность предвычисления приливных колебаний уровня зависит от числа волн, по которым ведётся расчёт. Для получения уровня с точностью ±1 см необходимо не менее 30 волн. При использовании только 11-ти основных гармоник рассчитывать на точность лучше, чем 10 % от величины прилива и ±10 мин. по времени наступления ПВ и МВ, не нужно.

ПРЕДВЫЧИСЛЕНИЕ ПРИЛИВОВ МЕТОДОМ СРАВНЕНИЯ

Предвычисление приливов по формуле (6.5) ведётся в пунктах, где в результате многолетних наблюдений за уровнем моря получены надёжные значения гармонических постоянных. Такие пункты называются основными в таблицах приливов, которые составляются на каждый год для этих пунктов. Однако существует много пунктов, в которых не ведутся постоянные наблюдения за уровнем, но предвычисление приливов необходимо там для обеспечения хозяйственной деятельности и судоходства. В таблицах приливов такие пункты называются дополнительными. Основной пункт для них подбирается из предположения, что колебания уровня в основном и дополнительном пункте схожие. Затем проводятся синхронные наблюдения за уровнем в этих пунктах (не менее 15 суток) и по ним находят для дополнительных пунктов поправки времен наступления полных и малых вод и поправки высот. Примеры предвычисления приливов для дополнительных пунктов подробно рассмотрены в таблицах приливов.

Многие порты расположены в устьевых участках рек. Подходные каналы к ним имеют, как правило, большую протяжённость. Высота прилива на различных участках таких портов (подходных каналов) будет отличаться от высоты прилива, измеренного на портовом водомерном посту. Особенно это характерно для мест, где подходной канал проходит по мелководным участкам. В таких случаях для точного определения глубины под килем необходимо и более точное значение высоты прилива. Проблема эта решается следующим образом. На протяжении всего подходного канала устанавливаются несколько водомерных постов и проводятся наблюдения. Сравнивая наблюдения в порту и на подходах к нему, находят для каждого участка поправки времени полных и малых вод и коэффициент прилива, представляющий собой отношение величины прилива в порту к величине прилива на подходах к нему.

Участки портовой акватории, для которых необходимо проводить описанные выше исследования, выбираются из условия: измеренная высота прилива на участке отличается от измеренной в порту в этот же момент времени на 0,1 м и более.

Приливные течения

Приливы везде сопровождаются приливными течениями. В приливной волне движение частиц воды происходит по эллиптическим орбитам с сильно вытянутой горизонтальной осью. Вертикальная составляющая движения частицы вызывает приливные колебания уровня, а горизонтальная составляющая обуславливает появление приливных течений. Эти течения, как и приливы, бывают полусуточными, суточными, смешанными и аномальными. Как и приливы, они обладают большой изменчивостью, что является следствием влияния рельефа дна, глубин, очертания береговой линии. По аналогии с приливными колебаниями уровня различают сизигийные и квадратурные приливные течения. Скорости течений в сизигию могут быть 2,5 раза больше, чем в квадратуру.

Приливные течения подвержены значительным пространственно-временным изменениям. Наглядное представление о том, как за время приливного цикла меняются скорость и направление течения, даёт годограф (от греч. Hodos — путь, движение) — кривая, которую описывает конец вектора течения, скорости которого в разные моменты времени отложены от произвольной точки. При построении годографа используют так называемое водное время. За нуль шкалы принимается момент наступления полной воды в ближайшем пункте, где ведутся постоянные наблюдения за приливами. В удалении от берегов приливное течение имеет вращательный характер: направление меняется постепенно от часа к часу, сохраняя более или менее одинаковую скорость.

С приближением к берегу под влиянием местных условий (рельеф дна, очертания берегов) с изменением направления заметно меняется и скорость течения: наблюдаются часы с минимальной и максимальной скоростями. Такие течения получили название вращающихся течений.

В реальных условиях годографы приливных течений имеют очень сложный характер (рис. 6.5).

В узких проливах, бухтах, устьях рек и т. п. приливные течения всегда направлены по одному и тому же “маршруту”, но в противоположных направлениях. Смена направления на противоположное происходит при достижении течением минимального значения. Такие течения получили название реверсивных.

Для предвычисления (прогноза) приливных течений используются результаты непосредственных наблюдений.

Эти наблюдения дают суммарные течения, из которых выделяют приливные, т. е. приливную составляющую, и остаточные течения, которые определяются как разность между суммарными и приливными течениями.

При правильных полусуточных или суточных приливах обработку данных наблюдений можно произвести одним из упрощённых методов (проекционный метод, метод И. В. Максимова, Северной гидрографической экспедиции и др.).

Суть методов состоит в следующем: из наблюдённых течений выделяют периодическую приливную составляющую. Делается это следующим образом. Предполагается, что за время периода скорость приливного течения меняется по синусоидальному закону. Отбираются данные ежечасных наблюдений за 13 часов при полусуточном характере течений и за 25 часов при суточном. Векторы скорости раскладывают на составляющие по меридиану и параллели, причём за положительное направление выбираются направления на север и восток. Сумма ежечасных значений скоростей за полный период должна равняться 0 в силу принятого допущения (синусоида). Но поскольку наблюдалось суммарное течение, то суммы не равны нулю, а равны конечной величине. Эта конечная величина представляет собой скорость суммарного течения, увеличенную во столько раз, сколько взято слагаемых. Следовательно, если полученную сумму разделить на число часов наблюдений, то мы получим скорость остаточного течения за период наблюдений. Теперь остаётся найти только разность между наблюдённым течением и остаточным на каждый час. Эта разность и будет представлять собой приливное течение.

Для расчёта любых приливных течений применяется гармонический анализ с тем отличием, что предварительно определяются составляющие измеренного течения на меридиан и параллель, как и при применении упрощённых методов. После этого находятся гармонические постоянные: амплитуды составляющих скорости на меридианы и параллель и специальные углы положения. Методика вычислений аналогична той, что применяется для обработки данных колебаний уровня. Гармонические постоянные в дальнейшем используются для предвычисления приливных течений.

Результаты предвычисления приливных течений представляются в виде атласов, карт и таблиц по лунному Т_л или водному Т_в времени. За нуль шкалы лунного времени принимается момент кульминации Луны Т_к на меридиане Гринвича; водного времени — момент наступления полной воды в пункте, где ведутся постоянные наблюдения за уровнем. Переход к поясному Т_п времени осуществляется по формулам:

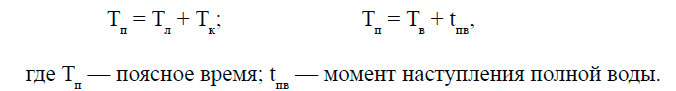
В настоящее время широко используются электронные версии таблиц приливов, карт приливных течений, совмещённые графики колебаний уровня и течений. В этом случае получить необходимые данные можно по любому удобному для пользователя времени.

Приближённо скорость максимального приливного течения можно определить по формуле:

где g — ускорение силы тяжести, м/с²; с = √gH — скорость распространения приливной волны, м/с; Н — глубина, м; ς — амплитуда прилива (половина величины прилива), м.

Скорости приливных течений в узкостях в исключительных случаях могут достигать 8–12 уз, а в некоторых норвежских фьордах — 14–16 уз. Это турбулентный поток с многочисленными вихрями, водоворотами, напоминающий бурную горную реку.

Литература

Гидрометеорологическое Обеспечение Мореплавания - Глухов В.Г., Гордиенко А.И., Шаронов А.Ю., Шматков В.А. [2014]

• Средства связи и сигнализации на судах
• Мореходные приборы и инструменты
• Окрасочные работы на судне
• Обязанности вахтенного матроса
• Пожарная безопасность судна