Морские течения

Классификация морских течений

Морскими течениями называются поступательные перемещения водных масс в морях и океанах, характеризующиеся направлением, скоростью и устойчивостью. Направление показывает, куда движутся водные массы, скорость задаётся в м/с или узлах. Устойчивость — это вероятность в процентах преобладающего направления. Эта характеристика была введена после того, как стало возможным проводить длительные (до года) наблюдения за течением в одной и той же точке. Оказалось, что направление течения меняется. Однако в некоторых случаях одно из направлений, как правило, наблюдалось чаще других. Оно и указывалось как направление течения в данной точке с определённой вероятностью (устойчивость).

Морские течения могут быть классифицированы по следующим признакам:

1. По силам, их вызывающим:

• ветровые или дрейфовые течения, возникающие в результате трения при движении ветра над поверхностью воды;
• градиентные течения, обусловленные горизонтальным градиентом давления, который возникает при наклоне поверхности моря относительно некоторой изопотенциальной (уровенной) поверхности. Градиенты давления могут создаваться изменением атмосферного давления и неравномерным распределением плотности морской воды в горизонтальном направлении;
• приливные течения, возникающие в результате воздействия на водные массы приливообразующих сил Луны и Солнца.

2. По устойчивости:

• постоянные или квазипостоянные — мало изменяются по скорости в течение сезона или года, наблюдаются в одних и тех же районах океана и характеризуются генеральным направлением (например, Гольфстрим);
• периодические — течения, направление и скорость которых повторяются через примерно равные промежутки времени и в определённой последовательности (приливные течения);
• непериодические (временные) — течения, вызванные непериодическим действием внешних сил (например, кратковременным действием ветра).

3. По глубине расположения:

• поверхностные — в слое воды от поверхности до глубины 10–15 м;
• подповерхностные — сразу же под поверхностным течением, но в направлении противоположном ему;
• придонные — в слое воды, прилегающем ко дну;
• глубинные — течения в толще воды между поверхностным и придонным.

4. По физико-химическим свойствам:

• тёплые — температура воды в течении выше, чем температура окружающих вод;
• холодные — температура воды в течении ниже температуры окружающих вод.

Течения с температурой окружающих вод иногда называют нейтральными.

Основы теории дрейфовых течений

В кинематике жидкостей применяются два различных метода описания движения: метод Лагранжа и метод Эйлера. В первом из них движение жидкости задаётся путём указания зависимости координат всех её частиц от времени.

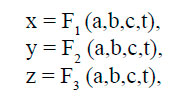
где a, b, c — координаты частицы в момент времени t = 0. Величины a, b, c и t называются переменными Лагранжа. Если из уравнений исключить время, то можно получить уравнение траектории частицы. Проекции на оси координат векторов скорости частицы будут равны:

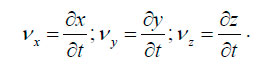
Метод Эйлера является основным в гидроаэродинамике. Движение жидкости определяется путём задания поля скоростей жидкости в пространстве:

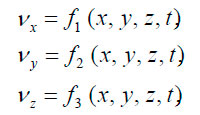
где v_x, v_y и v_z — проекции скорости жидкости по осям в момент времени t в точке пространства.

Запишем уравнение движения в декартовых координатах для составляющих по осям Ox и Oy. В таком виде оно называется уравнением Навье — Стокса:

В настоящее время система уравнений (4.1) не решается без кардинальных упрощений (допущений). Поэтому теоретическое решение расчёта скорости ветровых течений было выполнено Экманом при следующих допущениях:

• ρ = const;
• v_x ≠ 0, v_y ≠ 0, v_z = 0 — рассматривается только горизонтальное движение;
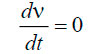• — движение установившееся;
• w = const — ветер постоянен по скорости и направлению;
• море безбрежно, поверхность горизонтальна, т. е.
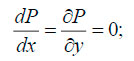
• вода несжимаема, море однородно по плотности. Это позволяет принимать во внимание только трение между горизонтальными слоями воды. Поэтому силу трения ветра о поверхность воды можно рассматривать как граничное значение внутренних сил трения при z = 0, т. е. на поверхности сила трения ветра (тангенциальное напряжение) будет равна:

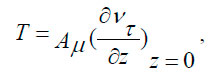
v_t — составляющая скорости течения в направлении ветра.

С учётом принятых допущений уравнения (4.1) принимают вид:

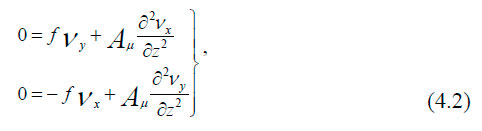
где f = 2ωsinφ — параметр Кориолиса; ω — угловая скорость вращения Земли; φ — географическая широта.

Таким образом, сила трения и сила Кориолиса на поверхности вращающейся Земли находятся в равновесии. Уравнения (4.2) имеют решения:

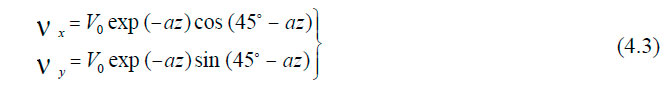
при условии, что ветер дует в северном направлении (T = T_yz).

Константы, входящие в уравнение, будут равны:

где V_о — абсолютная величина скорости течения на морской поверхности; ρ_w – плотность воды.

Анализ решения уравнений даёт нам следующие характеристики ветровых течений:

1. На поверхности z = 0.

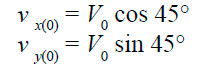
Таким образом, течение на поверхности V_о направлено на северо-восток. В общем случае в Северном полушарии поверхностное течение направлено под углом 45° вправо от направления дующего ветра, а в Южном — влево.

2. С удалением от поверхности z увеличивается, следовательно, V_о будет уменьшаться по закону

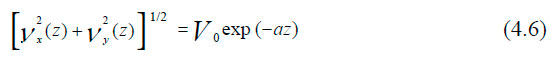
и поворачивать вправо в Северном полушарии.

3. Так как скорость течения уменьшается по экспоненте, то глубина, на которую распространяется течение, может быть выбрана произвольно. Экман предложил считать нижней границей такого слоя глубину, на которой вектор скорости течения направлен противоположно вектору поверхностной скорости:

Величина D известна в литературе как «слой Экмана».

Для вычисления силы трения ветра о поверхность воды Экман использует формулу:

где ρ_a — плотность воздуха, принимаемая равной
1,25 кг/м³; С — коэффициент трения, который был принят Экманом равным С = 1,6 × 10^-3; W₁₀ — скорость ветра, измеренная на высоте 10 м.

Для нахождения абсолютной скорости на поверхности воды V_о Экман воспользовался эмпирической формулой, которая, по-видимому, была ему известна из литературы:

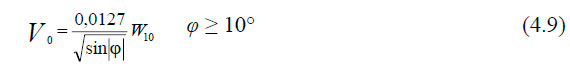
Затем, подставляя (4.9) и (4.8) в (4.4), находим A_μ и из уравнения (4.7) получаем:

В качестве примера в табл. 4.1 приведены вычисленные по формуле (4.10) толщины слоя Экмана для широт 15 и 45 градусов.

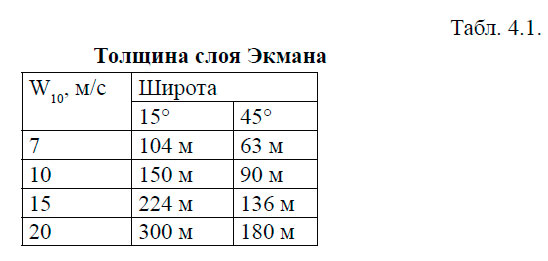
Работа Экмана была опубликована в 1905 г. И вот уже более 100 лет проблема изучения ветровой циркуляции продолжается. Для того, чтобы применить теоретические выводы Экмана к расчёту ветровых течений, необходимо знать два параметра: коэффициент турбулентной вязкости A_μ и силу трения ветра о поверхность воды Т (тангенциальное напряжение). Несмотря на большие успехи, достигнутые в изучении турбулентности и расчёта тангенциального напряжения, практически во всех учебниках, учебных пособиях и нормативных документах для расчёта ветровых течений рекомендуется формула (4.9). Авторство этой формулы не установлено. В некоторых работах просто указывается, что она получена по наблюдениям за сносом судов.

Специальные эксперименты для проверки теории Экмана были проведены в конце XX в. Эти эксперименты показали, что теория Экмана достаточно точно описывает течения на временных интервалах порядка нескольких суток. В частности, предположение об установившемся течении справедливо, когда продолжительность воздействия ветра превышает маятниковые сутки.

На основании экспериментов Ralph и Niiler получили следующие формулы для вычисления толщины слоя Экмана и абсолютной скорости поверхностного течения V_о:

Скорость ветра задаётся в м/с.

Таким образом, полученная толщина слоя D_Е практически совпадает со значением, вычисленным Экманом (4.10), а скорость поверхностного течения почти в два раза меньше (4.9).

Угол между направлением ветра и поверхностным течением зависит от широты; в средних широтах он составляет 45° (рис. 4.1).

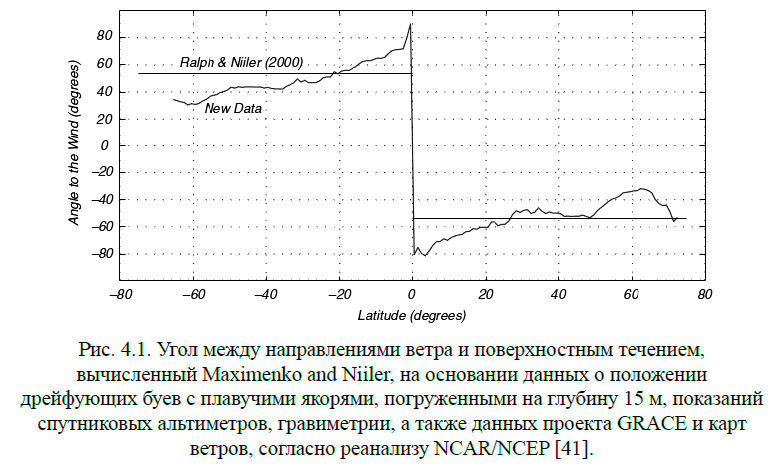
Основы теории геострофических течений

В толще воды океана, не испытывающей влияния приповерхностного слоя Экмана, в результате возникновения горизонтального градиента давления при наличии уклона водной поверхности развиваются геострофические (градиентные) течения. При горизонтальных масштабах, превышающих несколько десятков километров, и временных периодах свыше нескольких суток эта толща воды находится в состоянии геострофического равновесия. Это означает, что горизонтальный градиент давления почти полностью компенсируется силой Кориолиса, источником которой является развившееся течение. Для расчёта скорости геострофических течений требуется упростить уравнения (4.1).

Рассматривается установившееся течение в однородном по плотности океане, вязкие члены в уравнении движения пренебрежительно малы (силы внутреннего трения). Основные силы, действующие в вертикальном направлении — вертикальный градиент давления и сила тяжести, сбалансированы. В этом случае уравнения движения принимают вид:

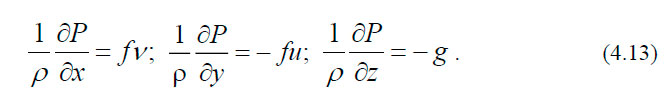
Эти уравнения известны как геострофические уравнения. Они применимы к потокам с горизонтальным масштабом, превышающим 50 км.

Уравнения (4.13) можно переписать в виде:

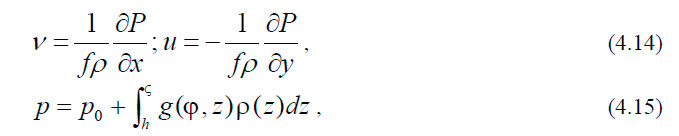
где p_o — атмосферное давление при z = 0; ς — возвышение морской поверхности над поверхностью z = 0; h — глубина.

При записи уравнений (4.13–4.15) принимается левая система координат: ось Oy направлена в сторону наибольшего уклона, а ось Oz — к центру Земли.

Подразумевается, что g зависит от широты и глубины, а ρ — от глубины.

Расчёт геострофических течений по альтиметрическим данным спутников

Система спутниковой альтиметрии состоит из радара, который измеряет высоту спутника над земной (морской) поверхностью, и системы слежения для определения высоты спутника в геоцентрической системе координат. Спутниковый альтиметр измеряет высоту спутника над поверхностью моря. Вычитая это значение из высоты орбиты, получаем уровень моря относительно центра Земли. Форма морской поверхности в спокойном состоянии практически совпадает с геоидом. В общем же случае она отклоняется от поверхности геоида под воздействием сил, вызывающих течения.

В слое небольшой толщины (несколько метров от поверхности) можно считать значения g и ρ постоянными. Тогда давление на уровенной поверхности, находящейся, например, на глубине 1 м будет равно:

Подставив (4.16) в уравнения (4.14), получаем выражения для составляющих скорости поверхностного течения u_п и v_п:

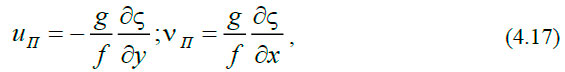
где g — ускорение силы тяжести; f — параметр Кориолиса; ς — возвышение уровня над уровенной поверхностью.

Таким образом, согласно уравнению (4.17) составляющие скорости поверхностного геострофического течения пропорциональны наклону морской поверхности. Если форма геоида нам известна, то величина наклона может быть измерена методами спутниковой альтиметрии (рис. 4.2).

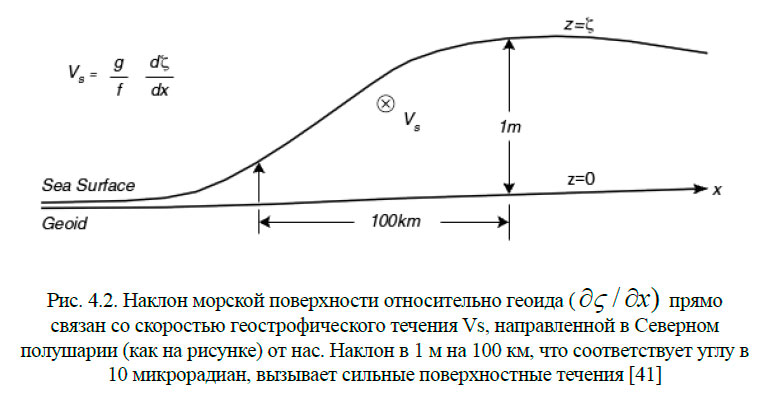
Исследование постоянных поверхностных течений проводится по альтиметрическим данным спутников, осреднённым за длительный период. Погрешность определения формы геоида при расчёте течений может быть существенной при осреднении на площади масштабом больше 100 км². Форма геоида достаточно хорошо изучена на более мелком масштабе (с пространственным разрешением больше 100 км) в результате специальных проектов по изучению гравитационного поля Земли GRACE и GOCE. Спутники этих проектов были запущены с российского космодрома Плисецк в 2002 и 2009 гг. соответственно. Спутники программы GOCE закончили работу в 2013 году. Одна из целей программы — определить геоид с точностью 1–2 см и достичь пространственного разрешения меньше 100 км. Эти системы проводят гравиметрические измерения с точностью, достаточной для того, чтобы не учитывать погрешность определения формы геоида.

Расчёт геострофических течений по океанографическим данным

Исследование геострофических течений по распределению температуры, солёности, плотности и давлению получил название динамического метода. В результате воздействия внешних сил формируется наклон поверхности моря и горизонтальная неоднородность плотности воды. Это приводит к возникновению горизонтального градиента давления. Возникает течение. Оно развивается и становится установившимся, т. е. сила горизонтального градиента уравновешивается силой Кориолиса. В отечественной литературе геострофические течения, обусловленные горизонтальным градиентом плотности воды, называются плотностными течениями. С помощью динамического метода можно рассчитывать не только поверхностные течения, но и глубинные.

Итак, движение вызывается градиентом горизонтального давления. Если бы мы имели совершенно определённую отсчётную поверхность (в предыдущем случае это геоид), то расчёт течений не представлял бы труда. Рассчитав поле плотности по уравнению состояния морской воды, можно было бы рассчитать давление в каждой точке, а затем течения по уравнениям (4.14, 4.15). В реальных условиях положение такой поверхности неизвестно. Поэтому все расчёты ведутся от так называемой «нулевой поверхности», т. е. предполагается, что на некоторой глубине существует поверхность, на которой горизонтальный градиент давления равен нулю.

Возьмём, например, глубину 1000 м на двух океанографических станциях (рис. 4.3 а). Между точками существует градиент давления Δp = pA − pB вследствие разности плотностей. Предположим, что ρ = const. Для того чтобы градиент сохранился, нужно поднять точку А и градиент давления будет обусловлен разностью высот ΔН, а линия А₁В будет представлять собой изобарическую поверхность (рис. 4.3 б).

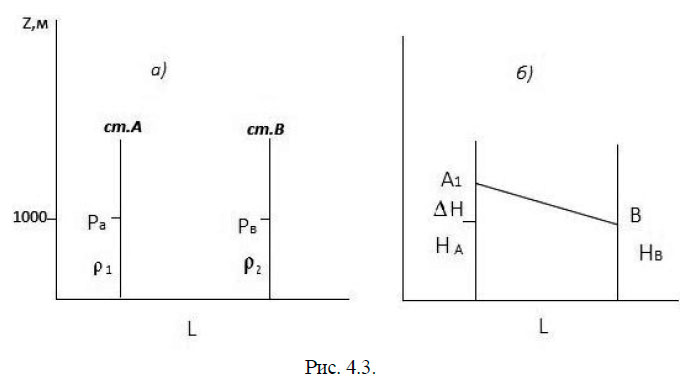
Следовательно:

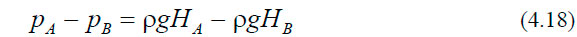
Величину gH = D по предложению Бьеркнеса принято называть динамической высотой. Динамическая высота — это не геометрическая величина, а работа, которую нужно совершить, чтобы переместить единицу массы по линии отвеса на расстояние Н. При измерении глубины в динамических метрах D = 0,1 gH, где Н — глубина в геометрических метрах. Динамическая высота используется как вертикальная координата z.

Таким образом, при вычислении скорости течения мы переходим от разности давления к разности динамических высот:

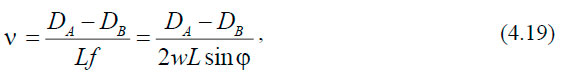
где L — расстояние между океанографическими станциями.

Течение направлено под углом 90° вправо от направления уклона в Северном полушарии и влево — в Южном.

При выводе формулы (4.19) было принято, что на глубине залегания нулевой поверхности течение отсутствует. Если это условие не соблюдается, то формула (4.19) будет содержать погрешность, равную неучтённой скорости течения на этой поверхности. Расчёт динамических глубин производится следующим образом:

изменение давления dp при изменении глубины на dH будет равно:

Далее в расчётах интеграл заменяется суммой, а вместо удельного объёма используется условный удельный объём v_t,s,p.

Подавляющее большинство расчётов течений динамическим методом выполнено относительно нулевой поверхности. Выбору этой поверхности посвящена обширная литература. Наиболее часто применяется метод, предложенный Дефантом. На графиках изменения с глубиной разностей динамических глубин изобарических плоскостей он обнаружил слой, в котором эти разности становятся постоянными. Дефант предположил, что этот слой почти неподвижен и принял его за слой, прилегающий к нулевой поверхности.

Границы применимости геострофических уравнений.

Принцип геострофического равновесия может быть применён к течениям протяжённостью в несколько сотен километров и временными периодами более нескольких суток. Равновесие подразумевает отсутствие какого-либо ускорения потока, а это означает, что течения в океанах никогда бы не изменялись. Важными ограничениями, которые присущи геострофическому приближению, являются:

1. Геострофические течения не могут изменяться во времени, поскольку установившееся течение не предполагает ускорения потока. При горизонтальных масштабах 50 км и менее ускорения потока неизбежны.
2. Геострофические уравнения не применимы в экваториальной полосе ±2°, где сила Кориолиса стремится к нулю (sinφ → 0).
3. Геострофическое равновесие не учитывает сил трения.
4. Динамический метод расчёта позволяет рассчитать течения только по отношению к нулевой поверхности, т. е. с течениями на другой глубине. Это может быть приемлемо для больших глубин. На небольших глубинах, например, в районе континентального шельфа он не слишком пригоден.

Точность расчётов. Сравнение измеренных и рассчитанных скоростей течений даёт следующие результаты. По данным спутниковой альтиметрии в системе течения Куросио на участке длиной 12,5 км разность между измеренными и рассчитанными течениями составила ±16 см/с для течений со скоростью до 150 см/с, т. е. около 10 %.

Сравнение измеренных скоростей и рассчитанных динамическим методом проводилось в системе течения Гольфстрим. Скорости, измеренные на глубинах до 500 м в центральных областях течения, были на 10–25 см/с больше, чем расчётные. Максимальная скорость в центре течения превышала 150 см/с. Таким образом, погрешность также составила около 10 %.

Основные черты поверхностной циркуляции вод Мирового океана

Осреднённые по времени поверхностные течения в океанах традиционно изображаются в виде «Схемы течений Мирового океана». В основу такой схемы положены главным образом данные океанографических наблюдений. Характерные черты океанической циркуляции рассмотрим на рис. 4.4, заимствованном из работы. Изображённая на схеме циркуляция вод соответствует современным представлениям о поверхностной циркуляции вод Мирового океана, основанным на данных, накопленных в течение более чем столетия наблюдений.

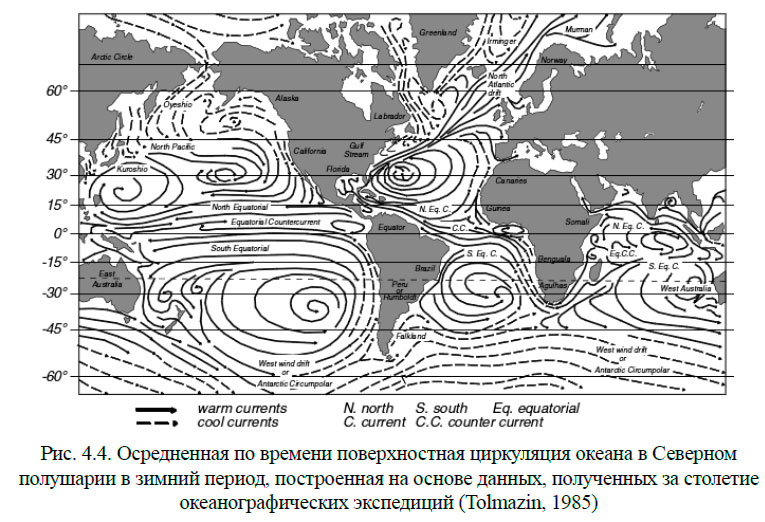
Течения поверхностных вод Атлантического и Тихого океана имеют много общих черт. В обоих океанах течения образуют два огромных антициклонических круговорота, которые разделяются экваториальными противотечениями. В южной части Индийского океана циркуляция в общих чертах сходна с циркуляцией в южных частях этих океанов. В северной части Индийского океана циркуляция обусловлена муссонами, и в периоды летнего и зимнего муссонов картина циркуляции полностью меняется.

Течения, образующие круговороты, значительно отличаются по скоростям на различных участках круговорота. Западные пограничные течения представляют собой узкие, глубокие, с чёткими границами потоки (Гольфстрим, Куросио).

Течения, направленные к экватору на другой стороне океанов — Бенгальское, Калифорнийское, Перуанское, — широкие, слабые потоки с расплывчатыми границами.

Экваториальные течения. Северное и Южное пассатные течения в Атлантическом и Тихом океане являются частью антициклонических круговоротов этих океанов. Между ними располагаются межпассатные противотечения, направленные на восток.

Южное пассатное течение, несущее воды на запад, существует и в южной части Индийского океана. В северной части океана располагается Муссонное течение, которое при северо-восточном муссоне направлено на запад. В этот период наблюдается и Межпассатное противотечение. В период юго-западного муссона направление Муссонного течения меняется на восточное.

В Южном полушарии отсутствие суши и широкий (300 миль) и глубокий (3000 м) пролив Дрейка между Южной Америкой и Антарктидой создают условия для беспрепятственного водообмена между всеми океанами в системе течения Западных ветров.

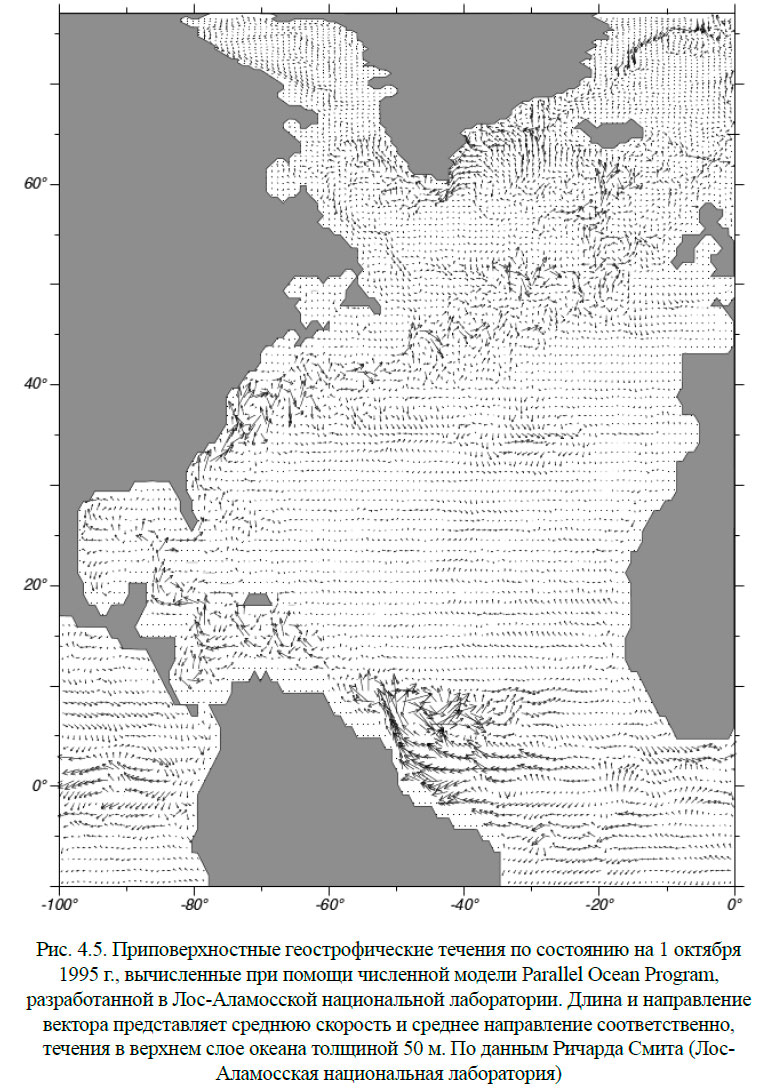
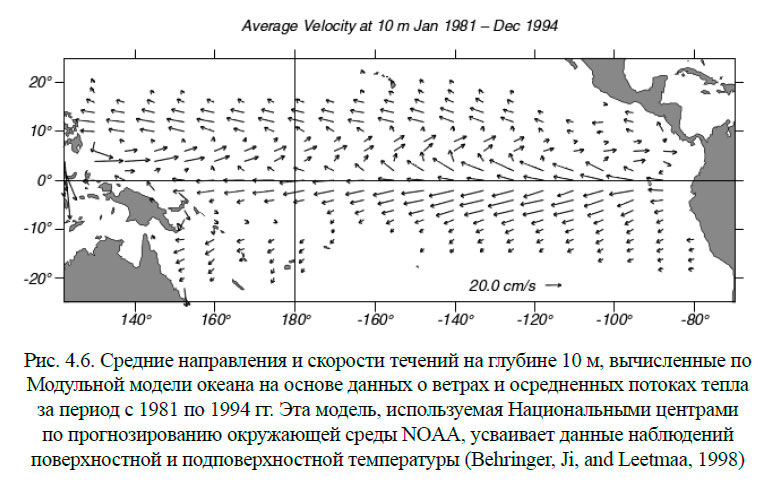
На современном этапе исследования глобальной системы океанических течений применяется математическое моделирование. Эти модели имитируют течения в реальном океане, с реальным рельефом дна, учитывают вязкость воды и нелинейные компоненты уравнения движения. Однако модели должны соответствовать возможностям современных компьютеров, а это означает, что в уравнения движения вносятся и будут и дальше вноситься различные упрощения (допущения). Существуют различные типы глобальных и региональных моделей Мирового океана. В заключение приведём два рисунка из работы (рис. 4.5, 4.6.). Читатель может самостоятельно сравнить их с рисунком (4.4).

Литература

Гидрометеорологическое Обеспечение Мореплавания - Глухов В.Г., Гордиенко А.И., Шаронов А.Ю., Шматков В.А. [2014]

• Средства связи и сигнализации на судах
• Мореходные приборы и инструменты
• Окрасочные работы на судне
• Обязанности вахтенного матроса
• Пожарная безопасность судна