Небесной сферой называют вспомогательную сферу, построенную произвольным радиусом, на которую спроектированы светила. За центр сферы обычно принимают точку О, соответствующую глазу наблюдателя. На рис. 6.1. изображена небесная сфера для наблюдателя, расположенного в некоторой точке земной поверхности в северной широте φ. Отвесная линия, проходящая через центр и совпадающая с направлением силы тяжести, пересекает небесную сферу в точках зенита «z» и надира «n». Плоскость, перпендикулярная отвесной линии и проходящая через центр сферы, называется плоскостью истинного горизонта, которая при пересечении с небесной сферой образует большой круг NESW.
Линия PNPS, параллельная оси вращения Земли, называется осью мира, а точки её пересечения с небесной сферой полюсами мира: северным PN и южным PS. Полюс, расположенный в надгоризонтной части сферы, называется повышенным, а в подгоризонтной — пониженным. Наименование повышенного полюса всегда одноименно с наименованием широты наблюдателя. Большой круг QEQ'W, плоскость которого перпендикулярна оси мира и проходит через центр сферы, называется небесным экватором.
Большой круг PNnPSz называется меридианом наблюдателя. Ось мира делит его на полуденную PNzPS и полуночную PNnPS части.
Большие круги PNCPS, плоскости которых проходят через полюсы мира, называют небесными меридианами, или кругами склонений. Большие круги zСn, плоскости которых проходят через отвесную линию (точки зенита и надира), называют вертикалами или кругами высоты. Вертикал, проходящий через точки Е и W, называется первым вертикалом.
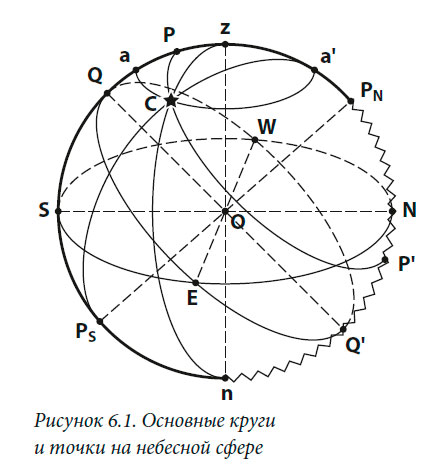
Малые круги PСР', плоскости которых параллельны плоскости небесного экватора, называются небесными параллелями. Малые круги аСа', плоскости которых параллельны плоскости истинного горизонта, называются альмукантаратами.
Плоскость экватора наклонна к плоскости горизонта под углом 90° — φ. Ось мира составляет с плоскостью истинного горизонта угол, равный географической широте φ места наблюдателя.
Горизонтная система координат
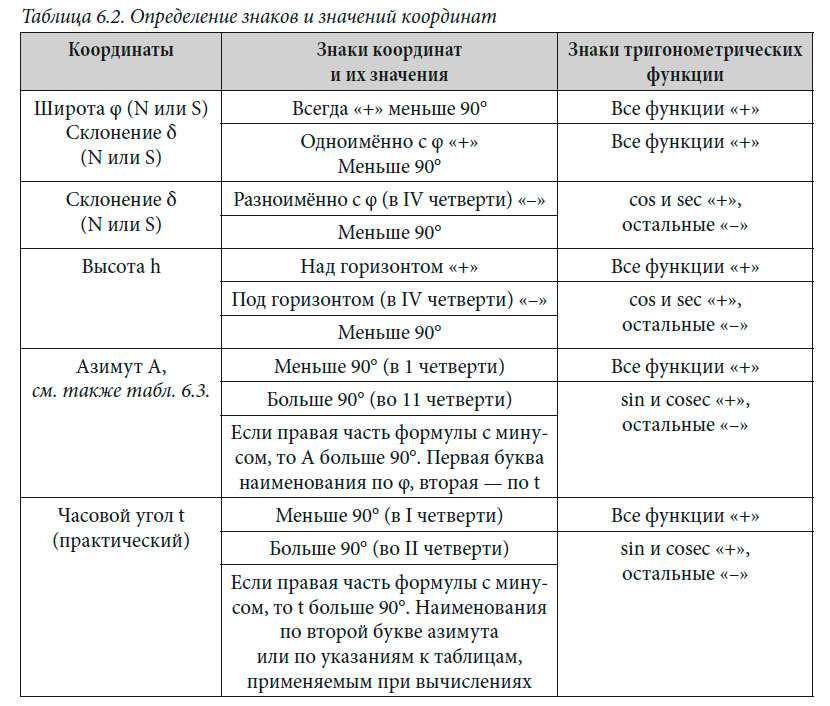
Азимут светила А — сферический угол при зените или дуга истинного горизонта между меридианом наблюдателя и вертикалом светила.
Применяются три системы счёта азимута. При полукруговом (практическом) счёте за точку начала отсчёта в северном полушарии принимают точку N, а в южном — точку S, т. е. точка начала отсчёта полукругового азимута всегда одноимённа с наименованием широты места наблюдателя. Азимуты ограничиваются пределом в 180°. При четвертном счёте азимуты отсчитываются от точек N и S в сторону Е и W от 0 до 90°. При круговом (навигационном) счёте азимут отсчитывается в любой широте от точки N в сторону Е от 0 до 360°.
Высота светила h — угол при центре небесной сферы или дуга круга высоты (вертикала) между истинным горизонтом и центром светила. Высота отсчитывается от 0 до +90° к зениту и от 0 до –90° к надиру. Отрицательная высота называется снижением светила. Дополнение высоты до 90°, т. е. дуга между зенитом и светилом, называется зенитным расстоянием z. Зенитное расстояние отсчитывается от зенита и изменяется от 0 до 180°.
Если светило находится на меридиане наблюдателя, то его высоту называют меридиональной высотой H, а зенитное расстояние — меридиональным зенитным расстоянием Z.
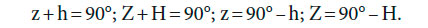
Первая система экваториальных координат
Часовой угол светила t — сферический угол при полюсе мира или дуга экватора между меридианами наблюдателя и светила.
Применяют две системы счёта часовых углов: обыкновенный, или вестовый,— часовой угол отсчитывается от полуденной части меридиана наблюдателя всегда в сторону W от 0 до 360°; практический — часовой угол отсчитывают от полуденной части меридиана наблюдателя в сторону точек Е или W от 0 до 180°. Вестовый часовой угол, если он превышает 180°, может быть переведён в практический остовый: tE = 360° – tW.
Склонение светила δ — угол при центре сферы между плоскостью небесного экватора и направлением на светило или дуга круга склонения (меридиана светила) от экватора до центра светила. Склонение измеряется от 0 до ±90°, ему приписывают наименование N, если светило находится в северной половине сферы, и наименование S, — если в южной. Склонение считают положительным, если оно одноимённо с широтой, и отрицательным, если оно разноимённо с широтой.
Вместо склонения иногда применяют его дополнение до 90°, т. е. дугу круга склонения от Северного полюса мира до светила, которая называется полярным расстоянием Δ. Полярное расстояние изменяется от 0 до 180°.
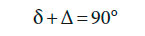
Вторая система экваториальных координат
Одной координатой в этой системе является, как и в первой, склонение светила δ, а в другой — прямое восхождение α — сферический угол при полюсе мира, измеряется дугой небесного экватора от точки весеннего равноденствия (точка Овна γ) в сторону, обратную вращению небесной сферы, до меридиана светила, т. е. в сторону движения Солнца по эклиптике.
Точка Овна находится на пересечении эклиптики с небесным экватором. В этой точке Солнце находится ежегодно 21 марта.
Эклиптика — плоскость, в которой движется Земля вокруг Солнца или большой круг небесной сферы (наклонённый к небесному экватору под углом 23°27'), по которому перемещается центр Солнца в его видимом годовом движении, отражающем движение Земли по её орбите.
Величина, дополняющая прямое восхождение до 360°, называется звёздным дополнением τ*.

Экваториальные координаты светил можно выбрать на любой момент из Морского Астрономического Ежегодника (МАЕ).
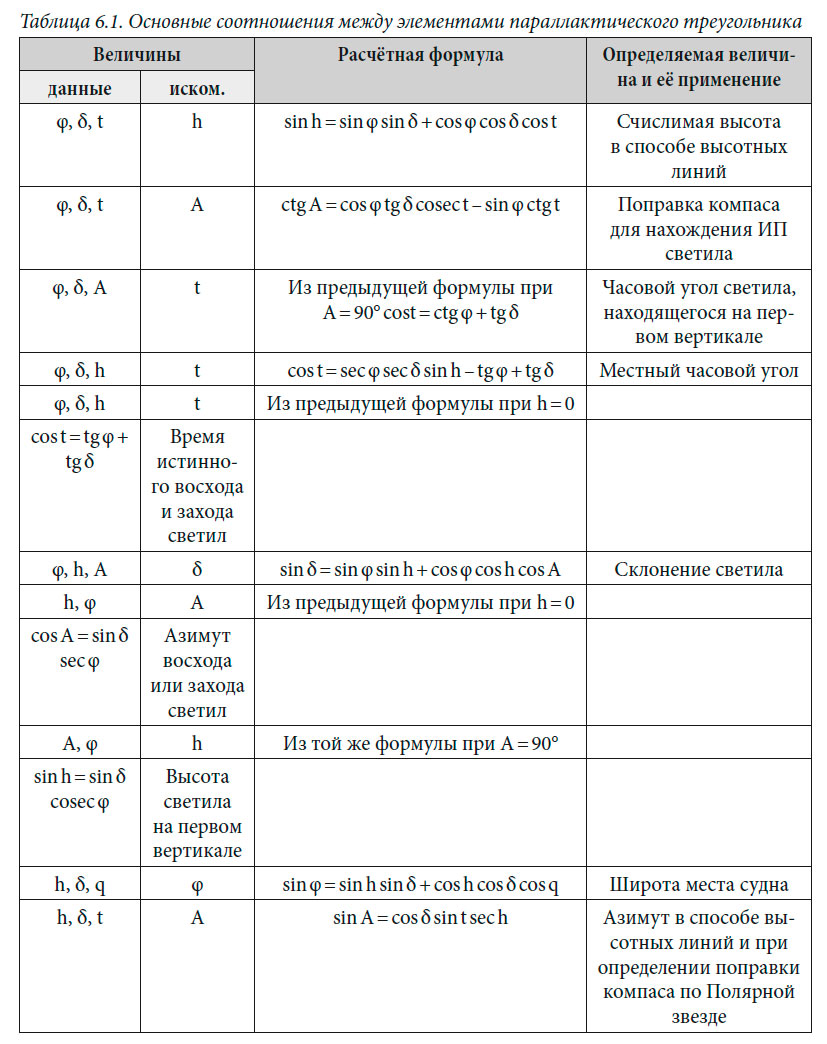
Параллактический треугольник и преобразование сферических координат
Сферический треугольник на небесной сфере, образованный пересечением меридиана наблюдателя, вертикала и меридиана светила, называется параллактическим или полярным треугольником светила. В зависимости от наименования широты места наблюдателя за постоянную вершину треугольника принимают повышенный Северный или пониженный Южный полюс мира (см. рис. 6.1.).

Координаты Солнца
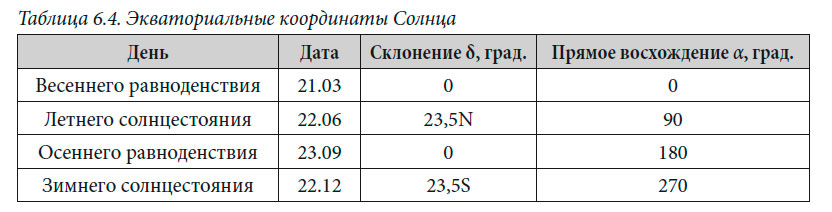
Суточное изменение склонения Солнца δ в течение месяца до и после дней весеннего и осеннего равноденствия равно 0,4°, в течение месяца до и после дней летнего и зимнего солнцестояний — 0,1°, в течение второго месяца после дней 21.03, 22.06, 23.09 и 22.12 — 0,3°.
Суточное изменение прямого восхождения Солнца α в течение всего года 1°. Точные значения координат на любой момент выбирают из Морского астрономического ежегодника (МАЕ).

Легко найти и даты начала и конца полярного дня и ночи. Приближённо условием начала и конца полярного дня принимают δ = 90° – (φ + 1°) при δ одноимённом с φ, а условием начала и конца полярной ночи δ = 90° – (φ – 1°), при δ разноимённом с φ.
Изменение φ на 1° приближённо учитывает полудиаметр Солнца и астрономическую рефракцию.
Например, в широте 75°N полярный день наступит и закончится при δ = 14° N, т. е. соответственно 1 мая и 13 августа, а полярная ночь будет длиться с 7 ноября до 5 февраля.
Литература
Справочник штурмана - Бурханов М.В [2010]

